Мета роботи. Ознайомитися з програмними реалізаціями додатків, що реалізують алгоритми оптимізації чи випадкового пошуку. Дослідити функції та можливості програм, здійснити низку експериментів, використовуючи різні значення параметрів, критеріїв чи навчальних наборів.
Генетичний алгоритм
Генетичні алгоритми виникли в результаті спостереження і спроб копіювання природних процесів, що відбуваються в світі живих організмів, зокрема, еволюції та пов'язаної з нею селекції (природного відбору) популяцій живих організмів.
Генетичний алгоритм - це метод, що відображає природну еволюцію методів вирішення проблем, і в першу чергу задач оптимізації. Його процедури пошуку засновані на механізмах природного відбору і спадкоємства. В них використовується еволюційний принцип виживання найбільш пристосованих особин. Вони відрізняються від традиційних методів оптимізації декількома базовими елементами.
Особливості генетичних алгоритмів:
- Обробляють не значення параметрів самого завдання, а їх закодовану форму.
- Здійснюють пошук рішення виходячи не з єдиної точки, а з їх деякої популяції.
- Використовують тільки цільову функцію, а не її похідні або іншу додаткову інформацію.
- Застосовують імовірнісні, а не детерміновані правила вибору.
Перелічені властивості приводять у результаті до стійкості генетичних алгоритмів і до їх переваги над іншими широко вживаними технологіями.
Класичний генетичний алгоритм складається з наступних кроків:
- Ініціалізація, або вибір вихідної популяції хромосом.
- Оцінка пристосованості хромосом в популяції.
- Перевірка умови зупинки алгоритму.
- Селекція хромосом.
- Застосування генетичних операторів.
- Формування нової популяції.
- Вибір «найкращої» хромосоми.
Генетичні алгоритми застосовуються при розробці програмного забезпечення, в системах штучного інтелекту, оптимізації, штучних нейронних мережах і в інших галузях знань. Прикладом може служити успішне розв'язання задачі комівояжера.
Рішення задачі комівояжера за допомогою генетичного алгоритму
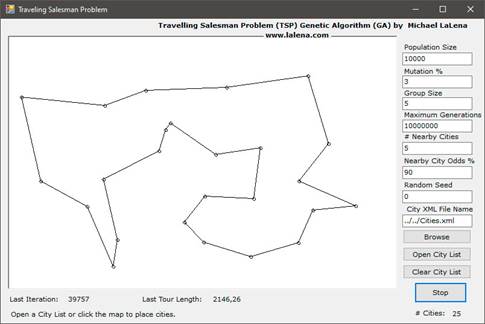
Задача комівояжера (Travelling salesman problem, TSP) - одна з найвідоміших задач комбінаторної оптимізації, що полягає у знаходженні самого вигідного маршруту, що проходить через зазначені міста хоча б по одному разу з наступним поверненням в початкове місто. В умовах задачі вказуються критерій вигідності маршруту (найкоротший, найдешевший, сукупний критерій тощо) і відповідні матриці відстаней, вартості і т. п. Як правило, вказується, що маршрут повинен проходити через кожне місто тільки один раз. Розроблено рішення задачі комівояжера (TSP) за допомогою генетичного алгоритму (ГА). У задачі комівояжера, мета - знайти найкоротшу відстань між N різними містами. Шлях, по якому продавець повинен пройти називається туром (рис.1).
Рис. 1. Інтерфейс програми TSP
Перевірка всіх варіантів проходження по N містах буде N!. Для розрахунку 30 турів по місту доведеться виміряти загальну відстань в 2,65 X 1032 різних турів. Припускаючи близько трильйона операцій в секунду, це займе 252.333.390.232.297 років. Додавання ще одного міста призведе до збільшення кількості розрахунків на 31!. Очевидно, що такий підхід неприпустимий.
Щоб знайти рішення за набагато коротший термін може бути використаний генетичний алгоритм,. Хоча він не може знайти краще рішення, він може стати практично ідеальним рішенням для розрахунку 100 турів через міста менше ніж за хвилину.
Основні кроки у вирішенні завдання комівояжера допомогою генетичного алгоритму.
- Створити групу з багатьох випадкових турів в початковій популяції. Цей алгоритм використовує жадібні обчислення для формування початкової популяції, віддаючи перевагу зв'язкам між містами, що знаходяться близько один до одного.
- Вибрати з двох кращих батьків (найкоротших турів) в популяції і скомбінувати їх, зробити двох нових нащадків. Сподіваючись, що ці нащадки будуть краще, ніж будь-який з батьків.
- З невеликою ймовірністю нащадки піддаються мутацї. Це робиться, щоб запобігти ідентичності всіх турів в популяції.
- Кращі нащадки (короткі тури) замінюють собою самі довжелезні тури в популяції. Чисельність особин в популяції залишається незмінною.
- Процес ітераційне повторюється до досягнення бажаної мети.
Як видно з назви, генетичні алгоритми імітують природу і еволюцію з використанням принципів виживання найбільш пристосованих особин.
Для вирішення завдання комівояжера з використанням генетичного алгоритму виникають основні проблеми: питання кодування туру і алгоритм кросовера, який використовується, щоб об'єднати двох батьків для отримання нащадків.
У стандартному генетичному алгоритмі, кросовер забезпечується випадковим вибором позиції в батьківській послідовності і обміном частин батьків. У цьому прикладі, точка перетину - між 3-м і 4-м пунктом списку.
| Батько 1 | FAB | ECGD |
|---|---|
| Батько 2 | DEA | CGBF |
| Нащадок 1 | FAB | CGBF |
| Нащадок 2 | DEA | ECGD |
Складність завдання комівояжера полягає в тому, що відвідати кожне місто в турі можна лише один раз. Якщо літери в наведеному вище прикладі представляють міста, тури-нащадки, що створені за цим кросовером, будуть вважатися недійсними. 1-й нащадок їде в місто F і B два рази, і ніколи не заїде в міста D або E.
Кодування не може бути просто списком міст в порядку, як вони були відвідані. Для цього створені інші методи кодування. Хоча ці методи не будуть створювати недійсні тури, вони не беруть до уваги той факт, що тур "ABCDEFG" такий же, як "GFEDCBA". Щоб вирішити цю проблему належним чином кросовер алгоритму повинен бути складніше.
Дане рішення зберігає посилання в обох напрямках для кожного туру. У наведеному вище прикладі про тури, новий батько 1 буде збережений як:
| Місто | Перша вершина | Друга вершина |
|---|---|---|
| A | F | B |
| B | A | E |
| C | E | G |
| D | G | F |
| E | B | C |
| F | D | A |
| G | C | D |
Кросовер операції набагато складніше, ніж поєднання двох рядків. Кросовер буде використовувати всі посилання, які є в обох батьків, і місце цих зв'язків в обох нащадках.
- Для Нащадку 1, вибір посилання буде у виборі серед Батька 2, а потім Батька 1.
- Для Нащадку 2, вибір складається з Батька 2 і Батька 1 з іншим набором посилань.
Для будь-якого нащадка, є ймовірність того, що посилання може створити недійсним тур, де замість одного шляху в турі буде створено багато розірваних турів. Ці посилання повинні бути відкинуті. Для заповнення решти відсутніх ланок, міста вибираються випадковим чином. Оскільки кросовер не є цілком випадковим, цей кросовер буде називатися жадібним.
Зрештою, ГА зробить так, що всі рішення будуть ідентичними. Це не є ідеальним рішенням. Якщо всі особини в ГА стануть ідентичними, ГА не зможе покращити рішення. Є два способи обійти це. Перший полягає у використанні дуже великих початкових розмірів популяції, так, що ГА буде потрібно багато часу, щоб все особини стали ідентичними. Другий метод - мутація, коли випадкові нащадки мутують, створюючи новий унікальний тур.
Цей генетичний алгоритм також використовує жадібні обчислення при розрахунку початкової популяції. Посилання на міста в первісному турі не є повністю випадковими. ГА воліє робити посилання між містами, які близькі один до одного. Це робиться на кожному кроці, інакше це зробило б всіх особин ідентичними.
Встановлено 6 параметрів для управління роботою генетичного алгоритму:
- Чисельність населення (Population Size) - чисельність популяції початкового числа випадкових турів, які створюються, коли алгоритм починає роботу. Велика кількість особин вимагає більше часу для знаходження результату. Менша кількість особин збільшується ймовірність того, що кожен тур до певної міри буде заміщати іншого і бути ідентичним. Це збільшує ймовірність того, що краще рішення не буде знайдено.
- Район / Розмір Групи (Neighborhood/Group Size) - Кожне покоління, це кількість турів, випадково обраних з популяції. 2 кращих тури будуть батьками, гірші 2 тури будуть замінені їх нащадками. Для великого розміру групи зростає ймовірність того, що в якості батьків будуть обрані дійсно хороші тури, але це також призводить до того, що багато турів ніколи не будуть використовуватися в якості батьків. Великий розмір групи приводить до швидшої роботи алгоритму, але він не може знайти найкраще рішення.
- Мутація % (Mutation %) - відсоток, що кожний нащадок після кросовера буде піддаватися мутації. Якщо до туру застосовано мутацію, тоді одне місто випадково пересувається з однієї точки в турі на іншу.
- # Довколишніх міст (# Nearby Cities) – Як частина жадібної початкової популяції, генетичний алгоритм при формуванні початкових турів надає перевагу зв’язці міст, які знаходяться близько один до одного. При створенні початкової популяції це число міст, які вважаються близькими.
- Поруч міста Коефіцієнти % (Nearby City Odds) - це процентна ймовірність, що будь-яке місто в випадковому турі в початковій популяції зволіють використовувати навколишні, а не абсолютно випадкові міста. Якщо генетичний алгоритм вибирає для використання навколишні міста, тобто в рівній мірі випадковість, що це буде одне з міст, у порівнянні з попереднім параметром.
- Максимум поколінь (Maximum Generations) – Скільки разів повторюється кросовер до завершення алгоритму.
Інші варіанти, які можуть бути налаштовані є (примітка: дані доступні тільки в завантажуваній версії):
- Випадкове ядро (Random Seed) - Це ядро для генератора випадкових чисел. Маючи фіксоване, а не випадкове ядро, можна повторити попередні результати з тими ж значеннями інших параметрів. Це корисно при пошуку помилок в алгоритмі.
- Перелік Міст (City List) – завантаження файлу, що дозволяє імпортувати списки з міста XML файлів. При з’ясуванні проблем, корисно мати можливість запускати алгоритм з тими ж точними параметрами.
Початкові значення параметра:
| Параметр | Початкове значення |
|---|---|
| Розмір популяції | 10,000 |
| Розмір групи | 5 |
| Мутації | 3% |
| Кількість сусідніх вершин | 5 |
| Коефіцієнти сусідніх міст | 90% |
Симулятори природних процесів
Симулятор еволюції автомобілів Rednuht
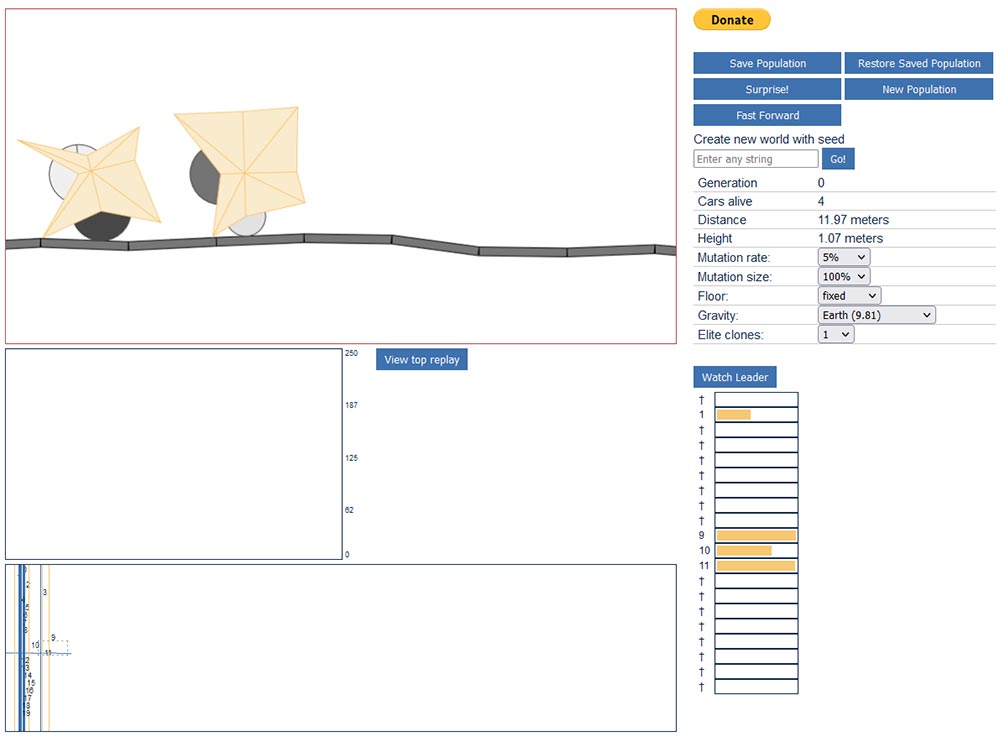
Простий браузерний симулятор, в якому можна простежити еволюцію простого двоколісного «автомобілю». Еволюційна програма генерує двохвимірний пристрої з коліс і кузовних деталей, мета яких - проїхати якомога довше по ламаній поверхні. Спеціальний алгоритм оцінює проходження траси кожним автомобілем. Наступні автомобілі генеруються вже з врахуванням попередніх вдалих, життєздатних екземплярів. Вони наочно еволюціонують - якщо в першому поколінні зразки без коліс не можуть проїхати і метра, то в третьому поколінні у них вже будуть з'являтися колеса і вдосконалюватися форма, а в десятому поколінні утворена машина буде здатна долати пристойні відстані. Пристосованість окремого рішення визначається відстанню, яку подолав пристрій від старту (рис.2).
Рис. 2. Інтерфейс симулятора генетичної еволюції автомобіля
Ця програма використовує генетичний алгоритм для розробки двовимірного автомобіля, який буде "оптимальним" для конкретної місцевості. Автомобіль має два колеса і два навантаження. Вихідні позиції і радіуси цих чотирьох об'єктів можуть бути вибрані за допомогою алгоритму. Об'єкти пов'язані пружинами, довжина яких так само обирається за алгоритмом. Навантаження ніколи не повинні торкатися землі.
Кожний автомобіль має геном, який містить інформацію про кожну з 8 вершин і кожне з 2 потенційних коліс. Також, окремий ген відповідає за те, які потенційні колеса виростають у машинки насправді.
У геномі автомобіля закодовано наступні параметри:
- Форма: 8 генів, що кодують вершини трикутників.
- Розмір коліс: 2 гена.
- Розміщення коліс: 2 гена.
- Щільність коліс: 2 гена.
- Щільність шасі: 2 гена.
При схрещуванні кожен ген береться випадковим чином від одного з батьків, а також з певною ймовірністю може мутувати, отримавши випадкове значення в заданому діапазоні. Особливим є лише ген, що визначає, які колеса виростають, а які ні. В ньому мутація полягає в тому, що може випадковим чином змінитися стан одного з коліс (виріс - не виріс), або інформація про колеса може зрушитися на біт вправо або вліво.
З симулятором можна погратися, задавши різні параметри еволюційного алгоритму. Наприклад, інтенсивність і величину мутацій, а також ступінь елітарності. Елітизм - збереження кращих особин з попереднього покоління, дозволяє не «розмивати» мутаціями знайдені хороші рішення. Симулятор одночасно запускає всю популяцію автомобілів, і можна спостерігати, як вони змагаються один з одним за право принести потомство.
Кольори показують кросинговер і мутацію для кожної особини популяції. Можна вибирати коефіцієнт мутації. Часто генеруються життєздатні моделі. Оптимальність часткового рішення (фітнес-функція придатності) визначається тим, наскільки довго воно існує, перш ніж:
- маса торкнеться землі;
- час закінчиться.
На початку, алгоритм навіть не знає, що колеса торкаються поверхні. Іноді можна побачити, як з'являються і зникають різні види - наприклад, "уніцикли", особливо на ранніх стадіях прогресу алгоритму.
Генетичні алгоритми можуть сходитися набагато швидше, при виборі фітнес-функції придатності, чисельності популяції. Розробник зробив моделювання більш цікавим стосовно візуалізації оптимізації, ніж швидким.
Симулятор Genetic Algorithm Walkers
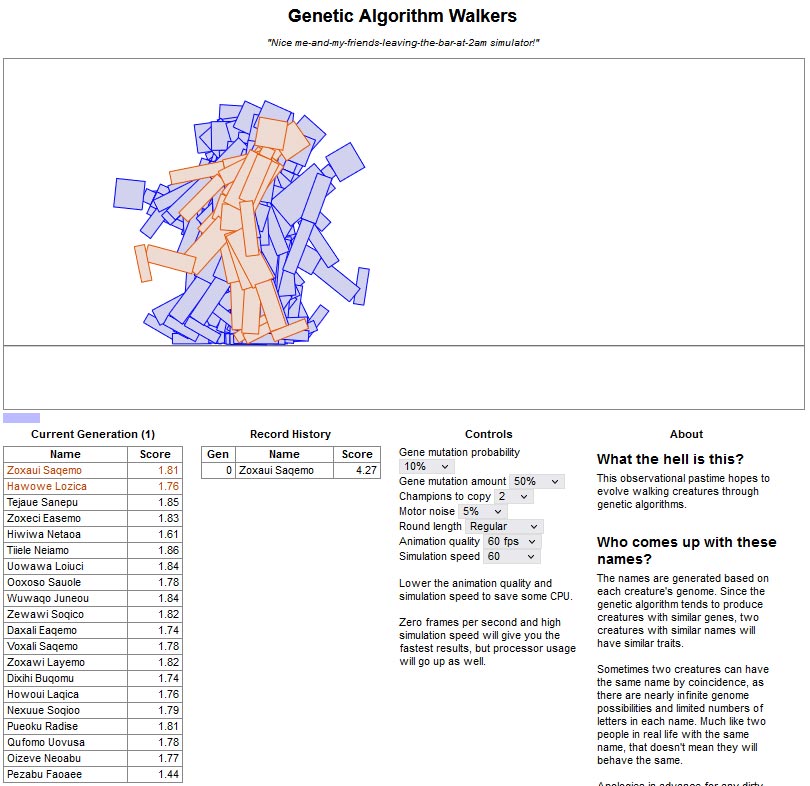
Genetic Algorithm Walkers пропонує спостерігати за процесом еволюції віртуальних роботів. Їх мета - зробити якомога більше кроків, на початку вони ледь стоять. Можна налаштувати ймовірність мутації, кількість мутацій і швидкість симуляції. Простежити за прогресом допоможуть таблиця рекордів і дані про робота покоління в даний момент (рис.3).
Після кожного раунду переможці переходять в наступне покоління і копіюються решта роботами з певними мутаціями. Від початку роботи симулятора темпи покращення є досить швидкими - протягом 100 поколінь, але чим далі, процес еволюції починає різко уповільнюватися.
Рис.3. Інтерфейс симулятора Genetic Algorithm Walkers
Симулятор Cambrian Explosion
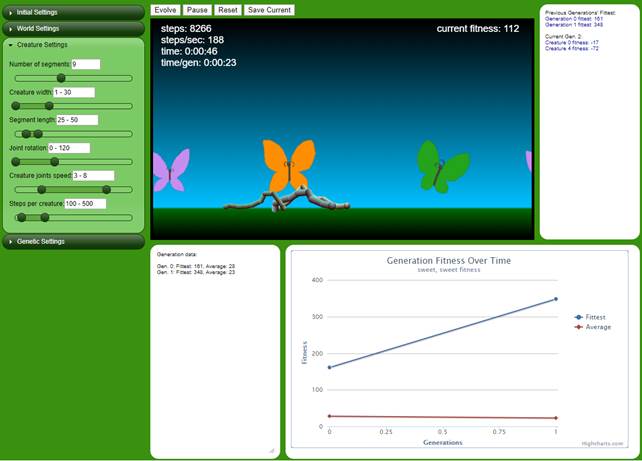
Симулятор «Камбрійський вибух» використовує генетичний алгоритм для розвитку руху в різних особин. В симуляторі передбачено багатий набір налаштувань характеристик особин та навколишнього середовища (рис. 4).
Для початку симуляції слід вибрати тип особини, за еволюцією яких потрібно спостерігати: хробак, кільце, зірка або чотиринога тварина. Найбільш цікаві результати демонструють хробаки і чотириногі. Далі можна налаштувати кількість особин, гравітацію в віртуальному світі, потенційний зовнішній вигляд особин, а також генетичні властивості, такі як ймовірність мутації і тип селекції. Після того, як всі налаштування виставлені, потрібно натиснути на кнопку «Evolve» і спостерігати, як особини вчаться ходити або повзати – внизу вікна відображається простий графік і інформація по поколіннях.
Рис.4. Інтерфейс симулятора Cambrian Explosion
Симулятор Світ ботів
Симулятор ботів, які будуть самостійно виживати в світі. Боти мають мозок (геном бота) - микропрограму, яка створюється і розвивається сама. Мозок - 64 комірки пам'яті (чисел). Кожне число – команда:
- Ходити.
- Повернутися.
- Схопити їжу або перетворити отруту в їжу.
- Подивитися, що є в сусідній комірці.
- Безумовний перехід.
- Далекий зір (бачити комірки, через сусідні).
На початку все комірки заповнюються випадковими числами, потім боти розміщують в середовище, де вони можуть за хід виконати від 1 до 10 команд (рис.6).
Якщо бот потрапив на їжу, йому додається 10 балів здоров'я, якщо на отруту - він помирає. Кожен хід бот втрачає 1 бал здоров'я. Коли здоров'я доходить до 0, бот відмирає.
Після кожної симуляції життя середовища нове покоління складають тільки кращі боти з попередньої симуляції і плюс додаються мутації (випадкової зміна декількох комірок пам'яті на випадкові числа).
Рис.6. Інтерфейс симулятора Genetic Bots
В результаті боти починають еволюціонувати і з кожним поколінням стають розумнішими.
Якщо пройти кілька поколінь (кілька тисяч), то боти вже цілком можуть жити. Для швидкої симуляції великої кількості поколінь - натиснути на кнопку Fast by Generations. Потім можна повернутися на Slow by Step.
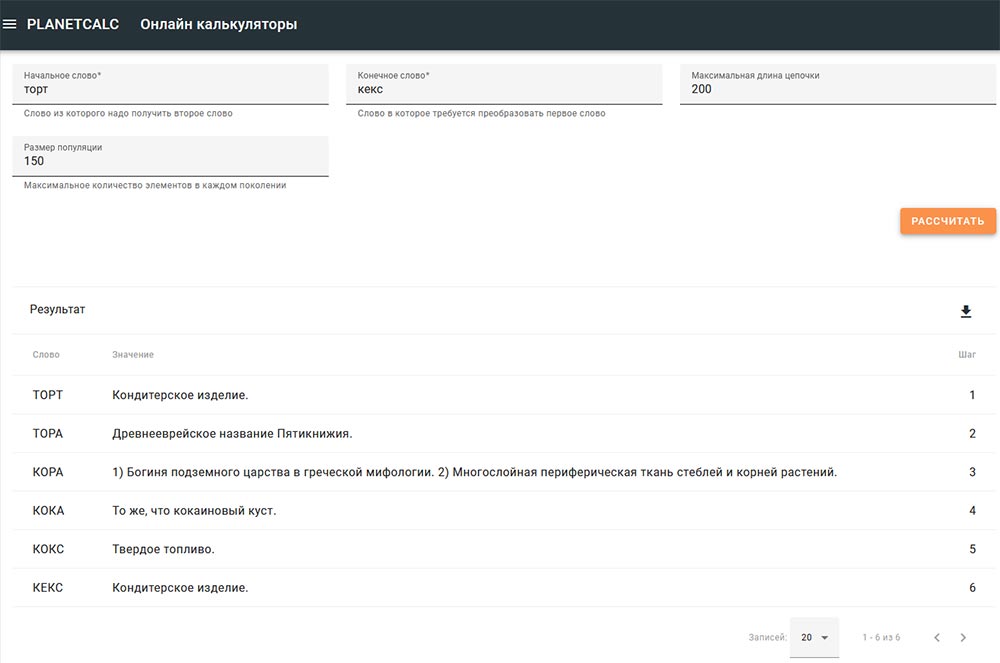
Перетворення слів за допомогою генетичного алгоритму. 4 літери та 5 літер
Емулятор покроково перетворює задане слово в інше задане слово, заміною однієї букви в попередньому слові, так щоб на кожному кроці виходило правильне слово. Емулятор працює зі словником, що містить слова, які складаються з 4 або 5 літер.
Користувач задає максимальну кількість поколінь і розмір популяції. Після обчислень на екран виводиться весь ланцюжок перетворень з тлумаченням кожного слова (рис.7).
Рис.7. Інтерфейс емулятора перетворення слів
У модифікованому генетичному алгоритмі застосовано покращену функцію селекції, яка відбирає лише самі подібні на кінцеве слово варіанти. Кількість життєздатних варіантів задається параметром «Розмір популяції», чим менше це число, тим швидше працює алгоритм, чим більше - тим якісніше виходить результат.
Як додатковий критерій зупинки введено обмеження на максимальний розмір ланцюжка. Алгоритм зупиниться, якщо після відтворення заданого числа поколінь не буде отриманий шуканий результат.
Функція пристосованості (подібності поточного слова на кінцеве) оцінювала кожне варіант за 12 бальною шкалою.
- За кожну літеру, що збігається з положенням і значенням з кінцевим результатом, нараховується 3 бали.
- Якщо голосна буква слова перебуває на тому ж місці, що й інша голосна буква шуканого слова - 2 бали.
- Один бал нараховується просто за наявність голосної букви.
Таким чином, кінцеве слово СЛОН оцінювалося в 12 балів, а початкова МУХА всього в 2.
Ройовий алгоритм птахів
Зграя птахів є чудовим прикладом колективної поведінки тварин. Літаючи великими групами, вони майже ніколи не стикаються в повітрі. Зграя рухається плавно і скоординовано, немов їй хтось керує. Якщо насипати зернят або крихти хліба для годування, за пару хвилин в цьому місці злітяться всі птахі в окрузі.
В зграях птахів зазвичай немає єдиного центру керування - ватажка, що віддає накази. Птахи в зграї діють згідно з визначеними, досить простими правилами. Узгоджена колективна поведінка птахів породжує ройовий інтелект зграї. Кружляючи в небі, кожний з птахів стежить за своїми родичами і координує свій рух згідно їх положенню.
Якщо хтось з птахів знайшовши джерело їжі, від сповіщає про це решта зі зграї. Причини такого «альтруїзму» птахів (і інших тварин, що діють подібним чином) були предметом дослідження багатьох соціобіології. Одним з найбільш популярних пояснень цього феномена є те, що переваги від такої поведінки кожної особини зграї більше, ніж такі очевидні недоліки, як необхідність боротьби за знайдену їжу з іншими особинами.
Джерела їжі, зазвичай, розташовані випадковим чином, тому, на самоті птах цілком може загинути, не знайшовши жодної крихти їжі протягом довгого часу. Однак якщо всі птахи будуть «грати за правилами», ділячись з родичами інформацією про знахідки, то шанси кожного з них на виживання різко підвищуються. Таким чином, будучи неефективною для окремої особини, така стратегія є запорукою ефективності зграї і виду в цілому.
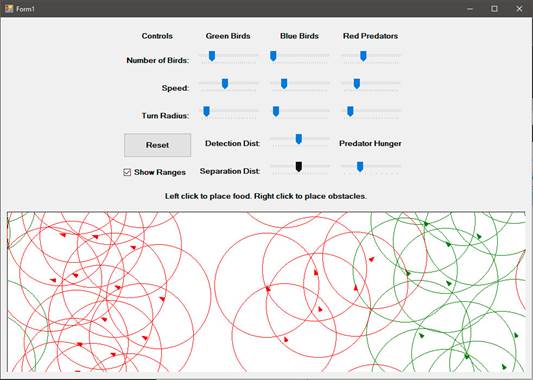
Спостереження за птахами надихнуло Крейга Рейнольдса (Craig Reynolds) на створення комп'ютерної моделі, яку він назвав Boids. Для імітації поведінки зграї птахів, запрограмовано поведінку кожного птаха окремо, а також їх взаємодію (рис.8).
Птахи дотримуються трьох простих правил алгоритму.
- Розділення: Кожен птах прагне уникнути зіткнень з іншими птахами.
- Вирівнювання: Птахи прагнуть рухатися на однаковій відстані одна від одної.
- Згуртованість: Кожен птах рухається в тому ж напрямку, що і навколишні птахи.
Розроблена поведінкова модель може бути розширена введенням додаткових чинників - таких, як пошук їжі або наявність хижаків.
В подальшому запропоновано метод для оптимізації безперервних нелінійних функцій, який назвали алгоритмом рою частинок, що заснований на управлінні дистанціями між птахами - а, отже, синхронність зграї є в них функцією від зусиль, які птиці докладають для збереження оптимальної дистанції.
Алгоритм рою частинок досить простий і може бути реалізований на будь-якій високорівневій мові програмування. Він моделює багатоагентну систему, де агенти-частинки рухаються до оптимальних рішень, обмінюючись при цьому інформацією з сусідами.
Поточний стан частинки характеризується координатами в просторі рішень (тобто, власне, пов'язаним з ними рішенням), а також вектором швидкості переміщення. Обидва цих параметра вибираються випадковим чином на етапі ініціалізації. Крім того, кожна частка зберігає координати одного з найкращих знайдених їй рішень, а також найкраще з пройдених усіма частинками рішень - цим імітується миттєвий обмін інформацією між птахами.
На кожній ітерації алгоритму напрямок і довжина вектору швидкості кожної з частинок змінюються у відповідності до відомостей про знайдені оптимуми:
ui = ui + a1 × rnd() × (pbesti - xi) + a2 × rnd() × (gbesti-xi)
де u - вектор швидкості частинки (ui - його i-а компонента), a1, a2 - постійні прискорення, pbest - найкраща знайдена часткою точка, gbesti - найкраща точка з пройдених всіма частинками системи, х - поточний стан частинки, а функція rnd() повертає випадкове число від 0 до 1 включно.
Після обчислення напрямку вектора, частка переміщається в точку. У разі необхідності, оновлюються значення кращих точок для кожної частки і для всіх частинок в цілому. Після цього цикл повторюється.
Рис.8. Інтерфейс демонстраційної програми Boids
 |
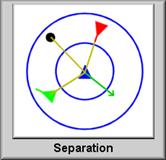
Виявлення птахів
Поки щось не потрапить у зону виявлення птахів, вони не реагуватиме на це. Не заплутайтеся у колах, що перекриваються (див. рис). У цьому прикладі птахи не можуть побачити один одного, поки сам птах не потрапить у коло виявлення інших птахів. |
 |
Розділення |
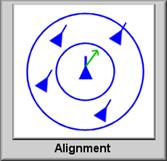 |
Вирівнювання |
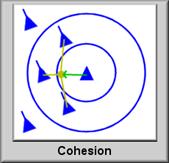 |
Згуртованість |
Алгоритм рою частинок широко застосовується в задачах машинного навчання, параметричної та структурної оптимізації (форм, розмірів і топології) в області проектування, в областях біохімії і біомеханіки. За ефективністю він може змагатися з іншими методами глобальної оптимізації, а низька алгоритмічна складність сприяє простоті його реалізації.
Відео лабораторної роботи
Контрольні запитання
- Назвати основні кроки в генетичному алгоритмі, як вони впливають на знаходження оптимальних результатів.
- Для вирішення яких завдань призначений генетичний алгоритм.
- Які корисні властивості надають особинам кросовер та мутація.
- Назвіть особливості і складності вирішення задачі комівояжера.
- Яким чином вирішується задача комівояжера за допомогою генетичного алгоритму.
- Які критерії вказують на життєздатність особини в еволюційних симуляторах.
- Які параметри надаються до регулювання у симуляторах еволюції автомобілів, роботів?
- Поясніть дії, що виконуються при перетворенні слів за допомогою генетичного алгоритму.
- Які особливості рою (зграї) використано при розробленні ройових алгоритмів.
- Для вирішення яких завдань здебільшого призначені ройові алгоритми.
Лабораторне завдання
- Ознайомитися з теоретичними матеріалами щодо природніх алгоритмів.
- Послідовно випробувати наведені сервіси, ознайомитися з інтерфейсом, можливостями сервісу і обмеженнями для пересічних користувачів. Здійснити низку досліджень в кожному з додатків: з параметрами, що встановлено за замовченням, зі зміненими параметрами.
- Проаналізувати отримані результати і з'ясувати причини відповідних розбіжностей.
- По результатах роботи оформити звіт.
- Під час захисту лабораторної роботи вільно володіти теоретичним матеріалом: особливості алгоритмів, усталені терміни, коло практичного застосування алгоритмів.
Зміст звіту
- Назва та мета виконання лабораторної роботи.
- Відповідно до кожного наданого додатку навести скріни з виконанням експериментів, висновки щодо зміни роботи алгоритмів за різних налаштувань.
- Аналітичні висновки щодо корисності та практичного застосування досліджених алгоритмів.